III
Spirala logarytmiczna jest to krzywa płaska przecinająca pod jednakowym, stałym kątem ? wszystkie półproste wychodzące z ustalonego punktu, zwanego biegunem spirali.
Spirala logarytmiczna to bardzo specyficzna krzywa, którą z pewnością wszyscy znają i nie raz się z nią spotkali, choć tak naprawdę nie znali jej tajemnej nazwy i z pewnością używali nazw typu: spiralka, zawijasek, zakrętas czy inne wymyślne sformułowania. Otacza nas wszędzie wokoło i co bystrzejsze spojrzenia z pewnością ją wychwycą. Już starożytni poznali ją, a fascynowała ludzi od wieków, a wręcz od pradziejów. Spirala to bardzo charakterystyczny "kształt", który rzuca się w oczy, wykorzystywały ją kultury i religie całego świata niezależnie od siebie, odnajdujemy ją w budowlach islamskich, katolickich, buddyjskich, możemy się jej doszukiwać w gotyku czy innych epokach i stylach architektonicznych, wiele malowideł, nawet obrazów takich autorów jak Da Vinci nie oparło się wpływowi logarytmów, które sprytnie się w nie wdarły.
Spirale logarytmiczne, odnalazły się praktycznie w budownictwie i architekturze, nie mówiąc już nawet o samych ozdobach, lecz całe kondygnacja są wzorowane na tym kształcie. Nasz "ślimaczek" istnieje w naszym świecie odkąd tylko ludzkość może cokolwiek spamiętać, lecz tak naprawdę to matematyka zajęła się jej badaniem
i zgłębieniem tajemnic. Z pewnością to nie my, ludzie, stworzyliśmy ten kształt, to on przyszedł do nas, jak wszystkie wzory, gdyż to natura wyznacza prawa, które my zaczerpujemy, odkrywamy i uczymy się na nich. A więc co do matematyki, teraz czeka was odrobinka wzorów (ludzie o słabych nerwach proszeni o pominięcie tego akapitu, zamykamy oczy razem z wami.
Matematyczny opis spirali logarytmicznej
Wzór, który opisuje spiralę logarytmiczną we współrzędnych biegunowych, gdy biegun spirali pokrywa się z początkiem układu współrzędnych:
lub 
gdzie:
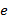to podstawa logarytmu naturalnego,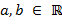
Jeden umowny koniec spirali logarytmicznej nawija się na biegun (dla 
spirala asymptotycznie zbliża się do bieguna 
), zaś drugi "ucieka"
w nieskończoność (dla 
zwoje spirali rosną nieograniczenie - 
).
Stosunek pochodnej wartości promienia r względem kąta ? do promienia jest stały i równy współczynnikowi w wykładniku:
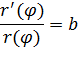
wobec czego kąt ? pomiędzy spiralą i promieniami (półprostymi) wychodzącymi
z bieguna spirali spełnia równość:
Zatem kąt ten jest stały i zarazem spełnia równość:
W tym przypadku współczynnik b decyduje o "szybkości" oraz kierunku skręcania spirali logarytmicznej. Gdy b=0 to kąt ?=???, -wtedy krzywa przecina promienie prostopadle i spirala przekształca się do okręgu o równaniu r=a. Gdy współczynnik b dąży do nieskończoności, to spirala po chłopsku "rozprostowuje się". Zmiana znaku przy współczynniku b, zmienia jednocześnie znak przy zmiennej ?, odwzorowując spiralę prawoskrętną w lewoskrętną i odwrotnie.
Współczynnik a oznacza skalą spirali, odpowiada zatem za jej wielkość. Zmiana wartości tego współczynnika odpowiada obracaniu spirali wokół bieguna według poniższego równania:
eb?-krotne zwiększenie współczynnika a odpowiada obróceniu spirali o kąt ?.
Równania parametryczne spirali logarytmicznej:
